5. Calculer avec numpy et scipy

Les librairies numpy et scipy contiennent tous les algorithmes usuels des calculs numériques. Nous allons en voir quelques uns.

5.1. Algèbre linéaire

numpy.linalg et scipy.linalg (plus de fonction dans scipy)

• Matrice : np.matrix (produit matriciel)

• Inverse de matrice

• Diagonalisation/valeurs propres/vecteurs propres

Avertissement

Le produit de deux tableaux np.array n’est pas le produit matriciel. Pour faire le produit matriciel, il faut utiliser l’opérateur “*” et des objets de type np.matrix ou utiliser l’opérateur @ (introduit dans Python 3.5).

Exemple: Calculer les valeurs propres de:

\[\begin{split}\begin{bmatrix} 1 & 1 & 0\\ 1 & 0 & 1 \\ 0 & 1 & -1\\ \end{bmatrix}\end{split}\]

import numpy as np
from scipy.linalg import eigh # Matrice hermicienne

H = np.matrix([[1, 1, 0], [1, 0, 1], [0, 1, -1]])

w, v = eigh(H)
print(w)
print(v)
print(H@v[:,1])

[-1.73205081  0.          1.73205081]
[[-0.21132487  0.57735027  0.78867513]
 [ 0.57735027 -0.57735027  0.57735027]
 [-0.78867513 -0.57735027  0.21132487]]
[[ 1.11022302e-16 -1.44328993e-15  1.55431223e-15]]

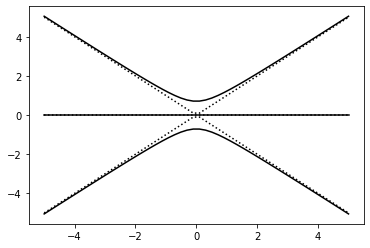
Tracer les valeurs propres en fonction de \(\delta\) pour \(\Omega=1\) de l’Hamiltonien suivant :

\[\begin{split}\begin{bmatrix} \delta & \frac\Omega2 & 0\\ \frac\Omega2 & 0 & \frac\Omega2 \\ 0 & \frac\Omega2 & -\delta\\ \end{bmatrix}\end{split}\]

import matplotlib.pyplot as plt

def trois_niveaux(delta, omega):
    H = np.matrix([[delta, omega/2, 0], [omega/2, 0, omega/2], [0, omega/2, -delta]])
    return eigh(H)[0]

all_delta = np.linspace(-5, 5)
sans_couplage = np.array([trois_niveaux(delta, omega=0) for delta in all_delta])
avec_couplage = np.array([trois_niveaux(delta, omega=1) for delta in all_delta])

plt.plot(all_delta, sans_couplage, 'k:')
plt.plot(all_delta, avec_couplage, 'k-');

5.2. Optimisation

5.2.1. Minimum d’une fonction

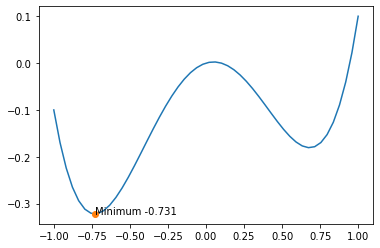
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fmin

def f(x):
    return 0.1*x + x**4 - x**2

x = np.linspace(-1, 1)
plt.plot(x, f(x))

x_min = fmin(f, -0.75)
plt.plot(x_min, f(x_min), 'o')
plt.text(x_min, f(x_min), f'Minimum {x_min[0]:.3f}');

Optimization terminated successfully.
         Current function value: -0.321919
         Iterations: 11
         Function evaluations: 22

5.2.2. Ajustement des moindre carrés

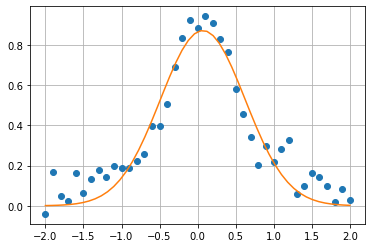
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

def fit_function(x, amplitude, largeur, centre):
    return amplitude*np.exp(-(x-centre)**2/(2*largeur**2))

X = np.linspace(-2, 2, 41)
data = 1/(1+(X-0.07)**2/.5**2) +  .05*np.random.normal(size=len(X))

plt.plot(X, data, 'o')

x_plot = np.linspace(-2, 2)
# Uncomment to see the curve with inital parameters
#plot(x_plot, fit_function(x_plot, amplitude=1,
#                         largeur=.5,
#                         centre=0))
init_param = [1, .5, 0]

popt, pcov = curve_fit(fit_function, X, data, init_param)
plt.plot(x_plot, fit_function(x_plot, *popt))
plt.grid()

5.3. Intégration

On peut utiliser la fonction quad

Exemple : calculer:

\[\int_0^{1} \frac{1}{1+x^2}\mathrm{d} x\]

from scipy.integrate import quad

def f(x):
    return 1/(1+x**2)

res, _ = quad(f, 0, 1)
print(res)

0.7853981633974484

Avertissement

Si on connaît la fonction, il ne faut pas en faire un tableau. La fonction quad calcule automatiquement les points de l’intégrale afin d’atteindre une erreur donnée. De plus, la fonction quad peut intégrer sur des bornes infinies (np.inf)

5.4. Equations différentielles

On utilise la fonction solve_ivp (initial value problem). Elle remplace les fonctions ode ou odeint

5.4.1. Equations du premier ordre

\[\frac{\mathrm{d}y}{\mathrm{d}t} = -\frac{y}{\tau}\]

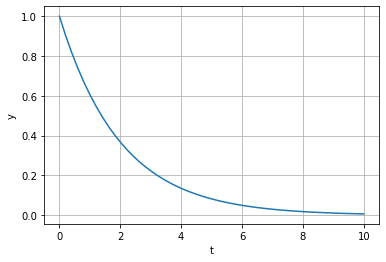
from scipy.integrate import solve_ivp
import numpy as np

tau = 2

def f(t, y):
    return -y/tau

y0 = 1
res = solve_ivp(f, t_span=[0, 10], y0=[1], t_eval=np.linspace(0, 10))

plt.plot(res.t, res.y[0,:])
plt.grid()
plt.xlabel('t')
plt.ylabel('y');

5.4.2. Équations différentielles d’ordre élevé

L’astuce consiste à augmenter la dimension de \(y\) en rajoutant des fonctions intermédiaires qui sont les dérivées de la fonction initiale.

Par exemple l’équation

\[\frac{d^2y}{dt^2} = \frac{f(y)}{m}\]

devient

\[\begin{split}\frac d{dt} \begin{pmatrix} y \\ y ^\prime \end{pmatrix} = \begin{pmatrix} y ^\prime \\ f(y)/m \end{pmatrix} = F(y, y^\prime)\end{split}\]

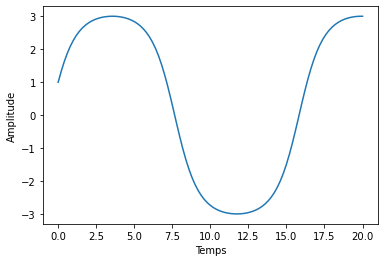
Voici comment résoudre l’équation d’un pendule \(\frac{d^2 \theta}{dt^2} = -sin(\theta)\):

def f(t, Y):
    y, v = Y
    a = -np.sin(y)
    return [v, a]

y0 = [1, 1.75]

res = solve_ivp(f, t_span=[0, 20], y0=y0, t_eval=np.linspace(0, 20, 101), rtol=1E-7, atol=1E-7)

plt.plot(res.t, res.y[0])
plt.xlabel('Temps')
plt.ylabel('Amplitude');

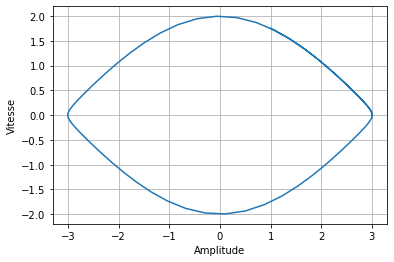
On peut aussi regarder la solution dans l’espace des phases :

plt.plot(res.y[0,:], res.y[1,:])
plt.grid()
plt.xlabel('Amplitude')
plt.ylabel('Vitesse');

5.5. Transformée de Fourrier

Le module numpy implément la transformée de Fourier numérique par l’algorithme de FFT. Pour cela, il faut utiliser les fonctions numpy.fft.fft et numpy.fft.ifft pour avoir la transformée de Fourier inverse. Lorsque l’on effectue un transformée de Fourier, l’axe des fréquences peut être obtenu à l’aide de la fonction numpy.fft.fftfreq.

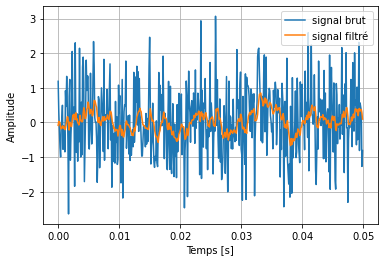
Voici un exemple de filtre passe bas utilisant la FFT

import numpy as np

dt = 1E-4
N = 50000
fc = 200
t = np.arange(N)*dt

# Simulation d'un signal
freq = 100
data = np.sin(2*np.pi*freq*t)*0.1 + np.random.normal(size=N)

# Réalisation d'un filtre dans l'espace de Fourier
data_tilde = np.fft.fft(data)
freq = np.fft.fftfreq(N, d=dt)
H = 1/(1+ 1J*freq/fc) # Fonction de transfert
data_tilde_filtre = data_tilde*H
data_filtre = np.real(np.fft.ifft(data_tilde_filtre))

from matplotlib.pyplot import figure

fig = figure()
ax = fig.subplots(1, 1)

ax.plot(t[:500], data[:500], label='signal brut')
ax.plot(t[:500], data_filtre[:500], label='signal filtré')
ax.set_xlabel('Temps [s]')
ax.set_ylabel('Amplitude')
ax.legend()
ax.grid()

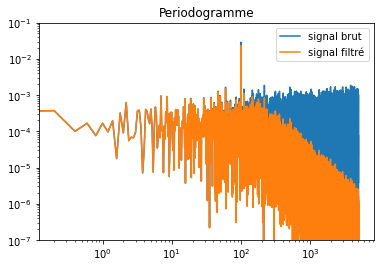
Souvent on a besoin d’évaluer la densité spectrale de puissance d’un signal. Il est possible pour cela d’utiliser la méthode du periodogramme avec la fonction scipy.signal.periodogram.

# On reprend le signal ci dessus
import scipy.signal
f, psd = scipy.signal.periodogram(data, fs=1/dt)
f, psd_filtre = scipy.signal.periodogram(data_filtre, fs=1/dt)

fig = figure()
ax = fig.subplots(1, 1)

ax.loglog(f, psd, label='signal brut')
ax.loglog(f, psd_filtre, label='signal filtré')
ax.set_title('Periodogramme')
ax.legend()
ax.set_ylim(1E-7, 1E-1);

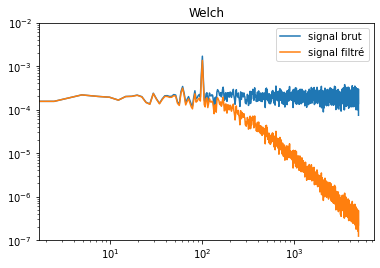
Il est aussi possible d’utiliser la méthode welch qui moyenne des periodogrammes pris sur des durées plus petites.

# On reprend le signal ci dessus
import scipy.signal
f, psd = scipy.signal.welch(data, fs=1/dt, nperseg=2**12)
f, psd_filtre = scipy.signal.welch(data_filtre, fs=1/dt, nperseg=2**12)

fig = figure()
ax = fig.subplots(1, 1)

ax.loglog(f, psd, label='signal brut')
ax.loglog(f, psd_filtre, label='signal filtré')
ax.set_title('Welch')
ax.legend()
ax.set_ylim(1E-7, 1E-2);