4. Tracer des graphiques

Nous utiliserons la librairie matplotlib. La fonctions sont dans le module matplotlib.pyplot qu’il est courant d’importer sous le nom de plt.

Le plus simple est d’étudier des exemples.

import matplotlib.pyplot as plt
import numpy as np

plt.figure(figsize=(10, 6))
X = np.linspace(-2,2, 100)
Y = np.sin(X)**2*np.exp(-X**2)
Y_noise = Y + .1*(np.random.rand(len(X))-0.5)

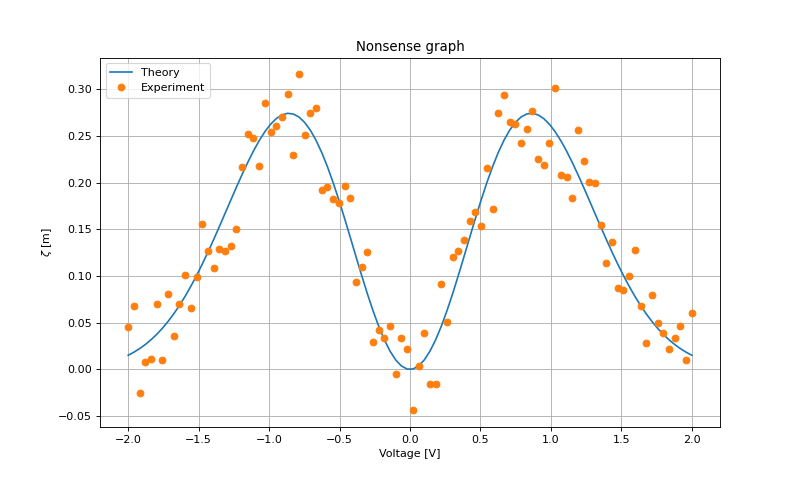
plt.plot(X,Y, label=u"Theory")
plt.plot(X,Y_noise,'o', label=u"Experiment")
plt.xlabel(r'Voltage [V]')
plt.ylabel(r'$\zeta$ [m]')
plt.title("Nonsense graph")
plt.legend(loc='upper left')
plt.grid(True)

plt.savefig('mafigure.pdf')

(Source code, png, hires.png, pdf)

Il existe deux syntaxes pour matplotlib, la syntaxe ci-dessus à base de fonctions (syntaxe historiquement utilisée par beaucoup de personnes) et une syntaxe utilisant sur des objets. L’idée est d’utiliser des méthodes des objets figure ainsi que des graphiques (appelé axes, il peut y avoir plusieurs axes, à ne pas confondre avec axis qui sont les abscisses et ordonnées).

Voici le même exemple en orienté objet:

from matplotlib.pyplot import figure
import numpy as np

fig = figure(figsize=(10, 6))
ax = fig.subplots(1, 1) # Création d'un graphique
X = np.linspace(-2,2, 100)
Y = np.sin(X)**2*np.exp(-X**2)
Y_noise = Y + .1*(np.random.rand(len(X))-0.5)

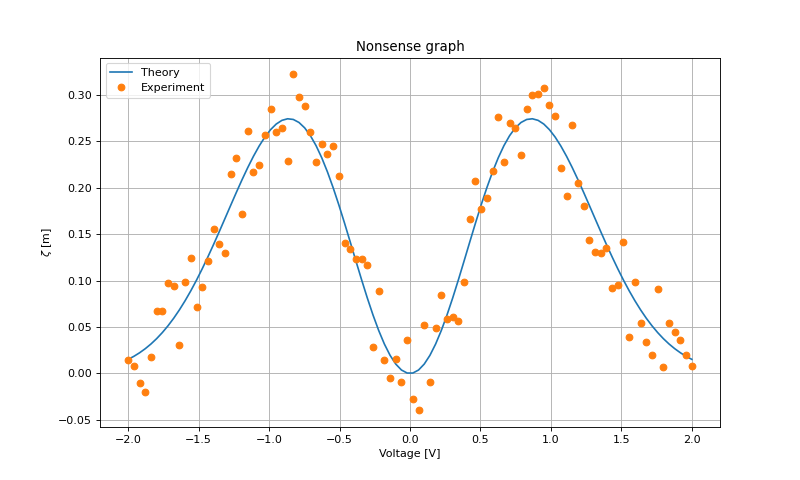
ax.plot(X,Y, label=u"Theory")
ax.plot(X,Y_noise,'o', label=u"Experiment")
ax.set_xlabel(r'Voltage [V]')
ax.set_ylabel(r'$\zeta$ [m]')
ax.set_title("Nonsense graph")
ax.legend(loc='upper left')
ax.grid(True)

(Source code, png, hires.png, pdf)

Le syntaxe orientée objet est plus simple lorsque l’on veut mettre plusieurs graphs dans une même figure.

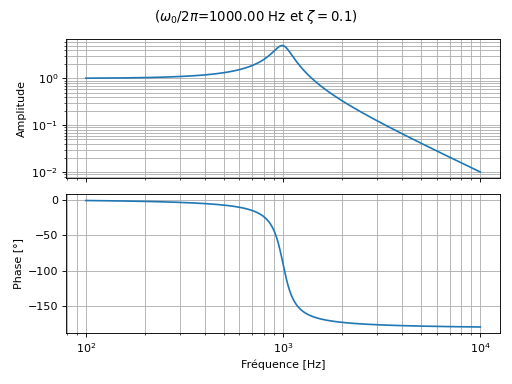
Voici un exemple du diagramme de Bode de la fonction de transfert suivante:

\[H(\omega) = \frac{\omega_0^2}{\omega_0^2 - \omega^2 + 2j\zeta\omega\omega_0}\]

import numpy as np
import matplotlib.pyplot as plt

# même pour une formule simple, il faut définir une fonction
def H(omega, omega_0, zeta):
    return omega_0**2/(omega_0**2-omega**2 + 2J*omega*zeta*omega_0)

omega_0 = 2*np.pi*1000
zeta = 0.1

Tomega = 2*np.pi*np.logspace(2,4, 1001)
amplitude = H(Tomega, omega_0, zeta)

fig = plt.figure()
ax1, ax2 = fig.subplots(2, 1, sharex=True)

fig.suptitle(f'($\omega_0/2\pi$={omega_0/(2*np.pi):.2f} Hz et $\zeta={zeta}$)')
ax1.grid(True, which='both')
ax1.loglog(Tomega/(2*np.pi), np.abs(amplitude))
ax1.set_ylabel('Amplitude')

phase_in_deg = np.unwrap(np.angle(amplitude))/(2*np.pi)*360

ax2.semilogx(Tomega/(2*np.pi), phase_in_deg)
ax2.set_ylabel(u'Phase [°]')
ax2.set_xlabel(u'Fréquence [Hz]')
ax2.grid(True, which='both')

fig.tight_layout()

(Source code, png, hires.png, pdf)

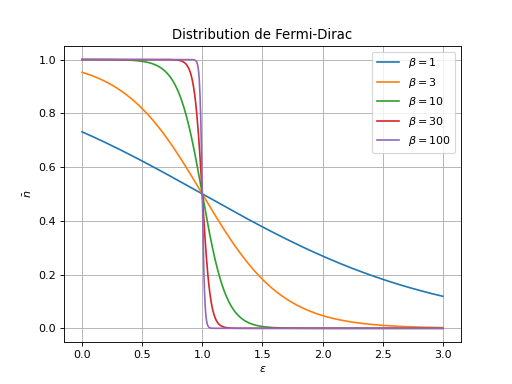
Graph avec des légendes : distribution de Fermi-Dirac

import numpy as np
import matplotlib.pyplot as plt

def fermi_dirac(epsilon, mu, beta):
    return 1/(np.exp(beta*(epsilon - mu))+1)

list_beta = [1, 3, 10, 30, 100]
mu = 1

x = np.linspace(0, 3, num=1000)

fig = plt.figure()
ax = fig.subplots(1, 1)

for beta in list_beta:
    ax.plot(x, fermi_dirac(x, mu=mu, beta=beta),
            label=rf'$\beta={beta}$')

ax.set_xlabel(r'$\epsilon$')
ax.set_ylabel(r'$\bar n$')
ax.set_title('Distribution de Fermi-Dirac')
ax.grid()
ax.legend()

(Source code, png, hires.png, pdf)

Remarques : pour les chaînes de caractère, il est possible d’utiliser des formules latex en utilisant des $. Il faut alors faire attention aux \ : en effet il est possible qu’ils soient interprété comme des caractères spéciaux (par exemple \n est un retour à la ligne). Pour éviter ceci, on utilise des chaîne brutes (raw string), préfixées par un r.

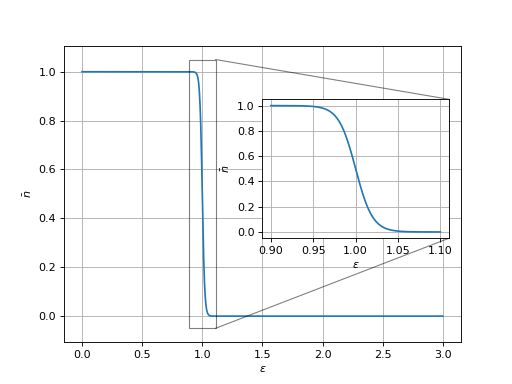
Figure avec un inset: distribution de Fermi-Dirac

import numpy as np
import matplotlib.pyplot as plt

def fermi_dirac(epsilon, mu, beta):
    return 1/(np.exp(beta*(epsilon - mu))+1)

x = np.linspace(0, 3, num=1000)
x_zoom = np.linspace(0.9, 1.1, num=1000)

fig = plt.figure()
ax = fig.subplots(1, 1)

ax.plot(x, fermi_dirac(x, mu=1, beta=100))

axins = ax.inset_axes([0.5, 0.35, 0.47, 0.47])
axins.plot(x_zoom, fermi_dirac(x_zoom, mu=1, beta=100))
ax.indicate_inset_zoom(axins, edgecolor="black")

for a in [ax, axins]:
    a.set_xlabel(r'$\epsilon$')
    a.set_ylabel(r'$\bar n$')
    a.grid()

(Source code, png, hires.png, pdf)

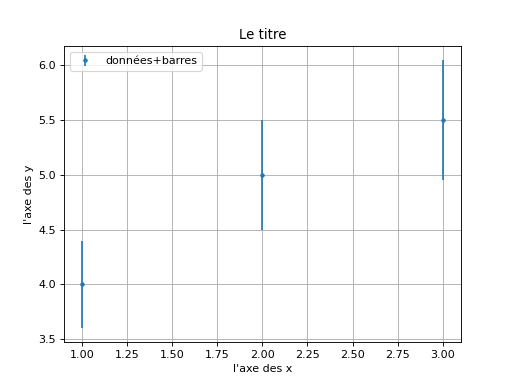
Barres d’erreur:

import numpy as np
import matplotlib.pyplot as plt

x = np.array([1, 2, 3])
y = np.array([4, 5, 5.5])
erreurs_y = 0.1 * y

plt.errorbar(x, y, erreurs_y, fmt='.', label="données+barres")

plt.xlabel("l'axe des x")
plt.ylabel("l'axe des y")
plt.legend(loc=2)
plt.grid()
plt.title("Le titre")

(Source code, png, hires.png, pdf)